Post test exponential and logarithmic functions – Embarking on an exploration of post-test exponential and logarithmic functions, this discourse delves into the significance of post-tests in evaluating student comprehension, highlighting their multifaceted benefits in assessing these intricate functions. By unraveling the diverse types, properties, and applications of exponential and logarithmic functions, we illuminate the path to enhanced understanding.
Through a comprehensive analysis of common misconceptions and challenges, we equip educators with strategies to effectively address these hurdles. Furthermore, we explore innovative pedagogical approaches and leverage technology to enhance student engagement and foster a deeper grasp of these fundamental mathematical concepts.
Post-Test Assessment of Exponential and Logarithmic Functions: Post Test Exponential And Logarithmic Functions
Post-tests play a crucial role in evaluating students’ understanding of exponential and logarithmic functions. They provide valuable insights into students’ strengths and weaknesses, allowing educators to tailor instruction and provide targeted support. Post-tests also serve as a formative assessment tool, helping students identify areas where they need additional practice and review.
Types of Post-Test Questions
- Multiple Choice:Assessing students’ basic understanding of key concepts and their ability to apply formulas.
- Short Answer:Requiring students to explain their reasoning and demonstrate their ability to solve problems involving exponential and logarithmic functions.
- Problem Solving:Evaluating students’ ability to apply their knowledge of exponential and logarithmic functions to real-world scenarios.
- Extended Response:Providing students with opportunities to demonstrate their higher-order thinking skills by analyzing and interpreting data related to exponential and logarithmic functions.
Types of Exponential and Logarithmic Functions
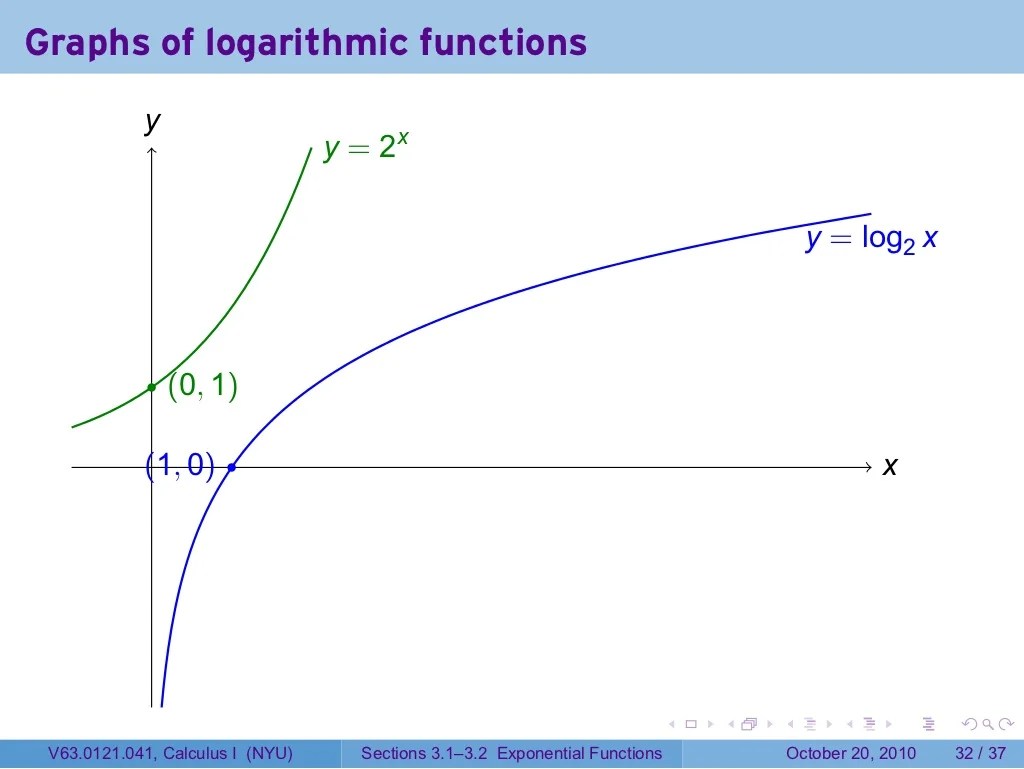
Exponential Functions, Post test exponential and logarithmic functions
- Natural Exponential Functions:Functions of the form y = e x, where e is the mathematical constant approximately equal to 2.71828.
- Exponential Functions with Bases Other Than e:Functions of the form y = a x, where a is any positive real number other than e.
Logarithmic Functions
- Natural Logarithmic Functions:Functions of the form y = ln(x), where ln is the natural logarithm with base e.
- Logarithmic Functions with Bases Other Than e:Functions of the form y = log a(x), where a is any positive real number other than e.
Properties of Exponential and Logarithmic Functions
Exponential Functions, Post test exponential and logarithmic functions
- Product Rule:a m· a n= a m+n
- Quotient Rule:a m/ a n= a m-n
- Power Rule:(a m) n= a mn
Logarithmic Functions
- Product Rule:log a(mn) = log a(m) + log a(n)
- Quotient Rule:log a(m/n) = log a(m) – log a(n)
- Power Rule:log a(m n) = n log a(m)
Applications of Exponential and Logarithmic Functions
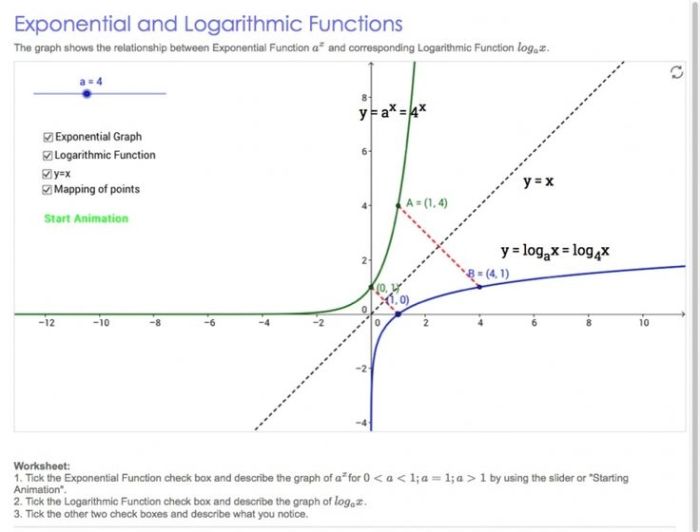
Exponential Functions, Post test exponential and logarithmic functions
- Population Growth:Modeling the growth of populations over time, where the rate of growth is proportional to the population size.
- Radioactive Decay:Describing the decay of radioactive substances, where the rate of decay is proportional to the amount of substance present.
- Compound Interest:Calculating the growth of investments over time, where the interest earned is compounded periodically.
Logarithmic Functions
- pH Calculations:Measuring the acidity or alkalinity of solutions, where the pH is the negative logarithm of the hydrogen ion concentration.
- Decibel Measurements:Quantifying the loudness of sounds, where the decibel level is the logarithm of the ratio of the sound intensity to a reference intensity.
- Richter Scale:Measuring the magnitude of earthquakes, where the Richter magnitude is the logarithm of the ground motion amplitude.
Common Misconceptions and Challenges
- Confusing Exponential and Logarithmic Functions:Students may struggle to distinguish between the two functions and their inverses.
- Misinterpreting Logarithmic Scales:Students may not understand the logarithmic scale and its implications for interpreting data.
- Applying Properties Incorrectly:Students may make errors when applying the properties of exponential and logarithmic functions, such as forgetting to convert to the same base before using the product or quotient rules.
Strategies for Addressing Misconceptions and Challenges
- Visual Representations:Using graphs, tables, and diagrams to illustrate the relationships between exponential and logarithmic functions.
- Real-World Examples:Connecting abstract concepts to real-world applications to enhance understanding and relevance.
- Step-by-Step Guidance:Providing clear and detailed instructions to guide students through problem-solving processes.
Teaching Strategies for Exponential and Logarithmic Functions
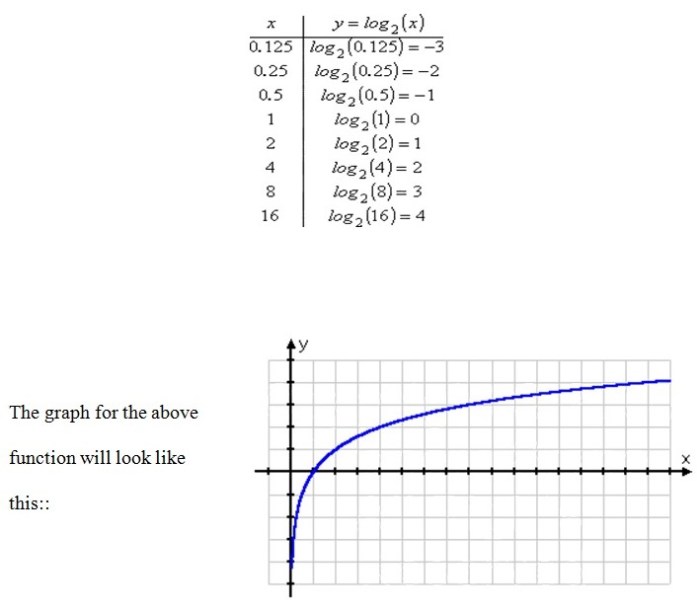
- Inquiry-Based Learning:Engaging students in hands-on activities and investigations to discover the properties and applications of exponential and logarithmic functions.
- Technology Integration:Utilizing graphing calculators and online simulations to visualize and explore these functions.
- Collaborative Projects:Encouraging students to work in groups on projects that involve modeling real-world phenomena using exponential and logarithmic functions.
Expert Answers
What are the key benefits of using post-tests to assess exponential and logarithmic functions?
Post-tests provide timely feedback on student understanding, allowing educators to pinpoint areas of strength and weakness, tailor instruction accordingly, and identify students who may require additional support.
What are some common misconceptions that students may have about exponential and logarithmic functions?
Students may mistakenly believe that exponential and logarithmic functions are inverses of each other, or that the base of an exponential function does not affect its graph. Additionally, they may struggle to understand the concept of logarithmic scales.
How can technology be integrated into the teaching of exponential and logarithmic functions?
Technology can enhance student engagement and understanding through interactive simulations, graphing calculators, and online resources that provide visual representations and real-time feedback.
